Sabun Köpüğünden Teknolojiye
Doç.Dr. M.Sami Polatöz
Çocuklar, sabun köpüğü ile oynamayı çok severler; genelde yuvarlak bir çerçeveyi sabunlu suyun içerisine daldırıp çıkartarak üfler ve baloncukların uçuşunu seyrederler. Sabun köpüğü ve sabun filmleri ile oynayanlar sadece çocuklar değildir. Bilim adamları yüzyıllardır sabun köpükleri ile deneyler yapmakta, matematik teorileri geliştirmekte, değişik yüzeyler elde ederek bu konudaki bilgileri teknolojiye aktarmaktadırlar.
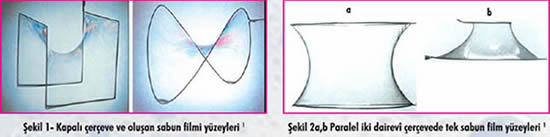
Sabun köpükleri ile oluşturulan yüzeylerin çok önemli bir özelliği vardır. Minimum yüzey-gerilim potansiyel enerjisine sahip olan bu yüzeyler, alan olarak da minimumdur. Bu yüzden sabun köpüklerinden oluşan alanlara ‘minimal alanlar’ denir. Kapalı bir çerçeve içerisindeki böyle bir alan, diğer oluşturulabilecek olanlardan her zaman daha az bir alanı işgal eder. Şekil 1’de iki farklı çerçeve ve oluşan alanlar gösterilmiştir. Her bir kapalı çerçeve için böyle en az bir minimal alan oluşturulabilir; bunun ispatlanması matematikçileri epey uğraştırmıştır.
Meşhur matematikçi Richard Courant (1888–1972) öğrencisi ile birlikte değişik çerçeveler kullanarak sabun köpüğü deneyleri yapmıştır.
Birden fazla kapalı çerçeve kullanılarak da minimal alanlar oluşturulabilir. İki daire şeklindeki çerçevenin birbirine paralel tutulması ile elde edilen minimal yüzeyler Şekil 2’de gösterilmiştir. Eğer çerçeveler birbirinden çok uzakta tutulursa hiç yüzey oluşmaz. Eğer yeterince yakın tutulurlarsa Şekil 2a ve 2b’dekine benzer yüzeyler elde edilir. Eğer çok yakın tutulurlarsa da Şekil 2c’deki gibi birbirine bitişik 3 minimal yüzey meydana gelebilir.
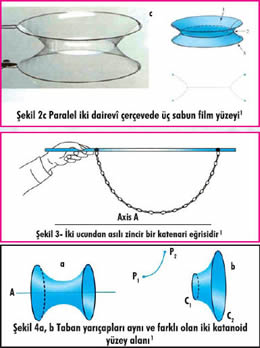
Tabiatta sadece canlı yapılarda değil cansızlarda da minimum enerji prensibi ile yaygın olarak karşılaşılmaktadır. Bir çubuğa zinciri iki noktadan Şekil 3’te olduğu gibi bağladığımızda zincir, çekim potansiyel enerjisini en az yapacak şekli alır. Bu yapıya (fonksiyona) matematikte katenari ismi verilir.
Katenari şeklinin bir A ekseni etrafında çevrilmesi ile oluşan döndürülmüş alanlara da katenoid denir. İki farklı katenoid Şekil 4a ve 4b’de gösterilmiştir. Katenoidler beklenildiği gibi minimal alanlardır ve sabun köpüğü kullanılarak elde edilebilirler. Bu tip yapılar eğer kullandığımız kaplarda tercih edilirse (bardak, tabak vb), en az ısı kaybına yol açacak ideal geometriler tasarlanabilir.
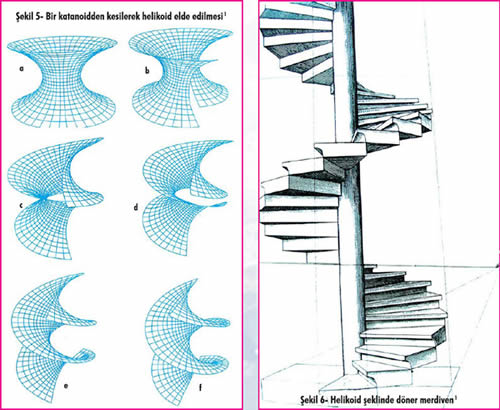
Şekil 5a’da gösterilen katanoid Şekil 5b’deki gibi bir kenarından kesilir, yavaşça uzatılarak döndürülürse en sonunda Şekil 5f’deki sarmal şekil veya helikoid elde edilir. Helikoid de minimal bir yüzeydir. Dönerek yükselen merdiven yapılarında mimarlar bu şekli sıkça kullanmışlardır (Şekil 6).
Ayrıca teknolojide çok kullanılan sonsuz vida sistemi de yine bu geometriye benzer bir yapıdadır.
Eğer bir helikoidi içine alabilecek en küçük hacimli silindir çizilir (Şekil 7a) ve yüzeyin silindir ile kesiştiği çizgiler işaretlenirse, çift heliks (Şekil 7b) yapısı elde edilir ki, bu, canlıların genetik yapı şifresi olan DNA moleküllerini modellemede kullanılır.
Sabun köpükleri ile ilgili iki temel kural vardır. Birincisi, eğer köpük kendisini destekleyen bir yüzey üzerinde ise bu yüzeye 900 açı yapacak şekilde birleşir. Düz bir yüzey üzerinde duran sabun köpüğü yarım küre şeklini alır ve her noktada destekleyen yüzey ile köpük yüzeyi 900 açılı olur. İkinci kural ise, eğer üç sabun köpüğü yüzeyi bir araya gelirse bir çizgi boyunda 1200 açı oluştururlar. Üç yüzeyin kesişmesi ile oluşan bu tip çizgilerden dört tanesi bir noktada bir araya gelirse, her iki çizgi arasındaki açı 1090 28’ 16’’ olur. Şekil 8’de bir tetrahedron çerçeve içerisinde oluşmuş bu tip yüzeyler gösterilmiştir.
900 ve 1200 açı prensiplerinin uygulanması ile matematikte önemli bir problem olan Steiner problemi çözülebilir. Steiner probleminde bir düzlemde verilen n adet noktayı birleştirecek en kısa yol ağı sorulmaktadır. Şeffaf iki düzlem, ince eşit uzunlukta paralel pimlerle birbirine bağlanarak bir sabun
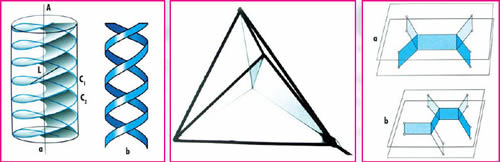
eriyiğine daldırılır. Çıkarıldığında düzlem filmleri oluştuğu görülür. Bu filmler şeffaf destekleyen düzlemlerle 900 açılıdır ve her üç sabun filmi bir araya geldiğinde, birbirleri ile 1200 açı meydana getirirler. Yukarıdan bakıldığında, sabun filmi ile yüzeylerden birisinin kesişim çizgileri n sayıda noktayı birleştiren en kısa ağı verir. Şekil 9a’da 4 noktanın, Şekil 9b’de ise 5 noktanın nasıl birleştirildiği gösterilmiştir. Akıl ve şuurdan yoksun sabun köpüğünün karmaşık bir matematik problemi kendiliğinden çözebilmesi mümkün olmadığına göre, ona, bu mükemmel davranış özelliğinin kazandırıldığını kabul etmek gerekir.
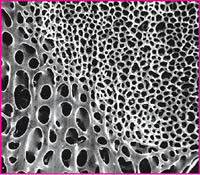
Denizkestanesi ve denizyıldızı gibi bazı deniz canlılarının iskeletinde organik ve inorganik maddeleri ayıran duvarlarda periyodik tekrarlanan minimal alanlara rastlanmıştır. Şekil 10’da denizkestanesi iskeletinin mikro yapısı gösterilmiştir. Bu geometrinin çatlak ilerlemesini engelleyecek mükemmel yapıda şekillendirildiği tespit edilmiştir.
Sabun köpüğü deneyleri mimarlar için de ilham kaynağı olmuştur. Çatı ve çadır tasarımlarında bu tip deneylerden faydalanılmıştır. Bu konuda en önemli isimlerden birisi Alman mimar Frei Otto’dur. Frei Otto’nun bir düzleme monte ettiği iğne ve saç inceliğindeki iplikleri sabunlu suya batırarak elde ettiği minimal alanlar Şekil 11’de gösterilmiştir.
Bu tip bir sabun köpüğü modelinin mimarî yapıya dönüştürülebilmesi için dikkatlice fotoğrafı çekilir ve hassas ölçümler yapılır. Bundan sonra katı modeller yapılır ve rüzgâr tünellerinde denenir. Özel ölçüm âletleri ile rüzgâr ve kar yükü altında oluşabilecek gerilmeler tespit edilir. Gerçek yapıda saç teli iplikçiklerinin yerini yüksek mukavemete sahip ince çelik kablolar alır. Sabun köpüğü zarının yerini ise şeffaf plâstik sentetik malzemeler alır.
Şekil 12’de Münih’teki Olimpiyat Stadı’nın çatısı, Şekil 13’te Münih’teki Olimpiyat Atletik Arena’nın çatısı, Şekil 14’te ise yine aynı şehirdeki Olimpik Yüzme Arenası’nın çatısı gösterilmiştir. Bütün bu çatılar sabun köpüğü deneylerinden elde edilen minimal yüzeyler kullanılarak yapılmıştır.
Çocuklar, sabun köpüğü ile oynamayı çok severler; genelde yuvarlak bir çerçeveyi sabunlu suyun içerisine daldırıp çıkartarak üfler ve baloncukların uçuşunu seyrederler. Sabun köpüğü ve sabun filmleri ile oynayanlar sadece çocuklar değildir. Bilim adamları yüzyıllardır sabun köpükleri ile deneyler yapmakta, matematik teorileri geliştirmekte, değişik yüzeyler elde ederek bu konudaki bilgileri teknolojiye aktarmaktadırlar.

2) Bu çatılar kolayca yükseltilebilir, sökülebilir ve başka yere taşınabilirler. Klâsik binalar ise bir yerden başka bir yere kolayca taşınamaz;
3) Hemen her yerinde çekme gerilme kuvvetleri hâkim olan bu yapılar çok sağlamdır. Klâsik binalarda ise basma gerilmeleri çok yoğun olup bu tip gerilmeleri karşılamak üzere beton, tuğla gibi yapıyı aşırı ağırlaştıran malzemeler kullanılır.

Hafif ve sağlam malzeme yapıları canlılarda mükemmel bir tarzda kullanılmıştır. Buna, iskelet sistemimizin hafiflikle dayanıklılığı bir araya getirmesi, buğday, arpa gibi narin bitkilerin saplarındaki mükemmel dayanıklılık, sinek kanadının son derece ince ve elâstik yapısı gibi binlerce misâl verilebilir. Bu konuda daha detaylı bilgi, kaynak 2’de mevcuttur. Alman mimar Frei Otto’nun bu konudaki bir sözü mânidârdır: “Biyoloji mimarlık için vazgeçilmez hâle gelmiştir. Mimarlık da biyoloji için vazgeçilmez hâle gelmiştir.” Sabun köpüğü gibi cansız yapılarda da benzer mükemmelliklerin görülmesi tabiattaki kanunların aynı elden çıktığını göstermektedir.
Bilgisayar kapasitelerinin çok artması ile minimal yüzeyleri bulmak daha kolay hâle gelmiştir. Sabun köpüğü deneylerine alternatif olarak bilgisayarlarca hesaplanan ve çizilebilen son derece karmaşık minimal yüzeyler elde edilmiştir. Eğer insanlık olarak bilim ve teknolojide ilerlemek istiyorsak, etrafımızdaki basit ve önemsiz gibi görünen hâdiselere daha dikkatle ve tefekkürle bakmamız, Yaradan’ın bize sunduğu güzellikleri ve mükemmellikleri keşfetmemiz ve insanlığın hizmetine sunmamız gerekmektedir. Tasarımlarımız ne kadar tabiatta işletilen kurallara uyumlu ise, başarı şansımız o kadar artacaktır.
Kaynaklar
1. S. Hilderbrandt, A. Tromba, The Parsimonious Universe, Springer-Verlag, New York, 1996.
2. M. S. Polatöz, Tabiatta Mühendislik, Kaynak Yayınları, İzmir, 2003.
3. A. B. Smith, The stereom microstructure of the echinoid test. Special Papers in Palaeontology, 25, 1-85, 1981.
[SES]http://www.sizinti.com.tr/dosyalar/sesler/64kbps/350/4078.mp3[/SES]
Doç.Dr. M.Sami Polatöz
Çocuklar, sabun köpüğü ile oynamayı çok severler; genelde yuvarlak bir çerçeveyi sabunlu suyun içerisine daldırıp çıkartarak üfler ve baloncukların uçuşunu seyrederler. Sabun köpüğü ve sabun filmleri ile oynayanlar sadece çocuklar değildir. Bilim adamları yüzyıllardır sabun köpükleri ile deneyler yapmakta, matematik teorileri geliştirmekte, değişik yüzeyler elde ederek bu konudaki bilgileri teknolojiye aktarmaktadırlar.
Sabun köpükleri ile oluşturulan yüzeylerin çok önemli bir özelliği vardır. Minimum yüzey-gerilim potansiyel enerjisine sahip olan bu yüzeyler, alan olarak da minimumdur. Bu yüzden sabun köpüklerinden oluşan alanlara ‘minimal alanlar’ denir. Kapalı bir çerçeve içerisindeki böyle bir alan, diğer oluşturulabilecek olanlardan her zaman daha az bir alanı işgal eder. Şekil 1’de iki farklı çerçeve ve oluşan alanlar gösterilmiştir. Her bir kapalı çerçeve için böyle en az bir minimal alan oluşturulabilir; bunun ispatlanması matematikçileri epey uğraştırmıştır.
Meşhur matematikçi Richard Courant (1888–1972) öğrencisi ile birlikte değişik çerçeveler kullanarak sabun köpüğü deneyleri yapmıştır.
Birden fazla kapalı çerçeve kullanılarak da minimal alanlar oluşturulabilir. İki daire şeklindeki çerçevenin birbirine paralel tutulması ile elde edilen minimal yüzeyler Şekil 2’de gösterilmiştir. Eğer çerçeveler birbirinden çok uzakta tutulursa hiç yüzey oluşmaz. Eğer yeterince yakın tutulurlarsa Şekil 2a ve 2b’dekine benzer yüzeyler elde edilir. Eğer çok yakın tutulurlarsa da Şekil 2c’deki gibi birbirine bitişik 3 minimal yüzey meydana gelebilir.
Tabiatta sadece canlı yapılarda değil cansızlarda da minimum enerji prensibi ile yaygın olarak karşılaşılmaktadır. Bir çubuğa zinciri iki noktadan Şekil 3’te olduğu gibi bağladığımızda zincir, çekim potansiyel enerjisini en az yapacak şekli alır. Bu yapıya (fonksiyona) matematikte katenari ismi verilir.
Katenari şeklinin bir A ekseni etrafında çevrilmesi ile oluşan döndürülmüş alanlara da katenoid denir. İki farklı katenoid Şekil 4a ve 4b’de gösterilmiştir. Katenoidler beklenildiği gibi minimal alanlardır ve sabun köpüğü kullanılarak elde edilebilirler. Bu tip yapılar eğer kullandığımız kaplarda tercih edilirse (bardak, tabak vb), en az ısı kaybına yol açacak ideal geometriler tasarlanabilir.
Şekil 5a’da gösterilen katanoid Şekil 5b’deki gibi bir kenarından kesilir, yavaşça uzatılarak döndürülürse en sonunda Şekil 5f’deki sarmal şekil veya helikoid elde edilir. Helikoid de minimal bir yüzeydir. Dönerek yükselen merdiven yapılarında mimarlar bu şekli sıkça kullanmışlardır (Şekil 6).

Ayrıca teknolojide çok kullanılan sonsuz vida sistemi de yine bu geometriye benzer bir yapıdadır.
Eğer bir helikoidi içine alabilecek en küçük hacimli silindir çizilir (Şekil 7a) ve yüzeyin silindir ile kesiştiği çizgiler işaretlenirse, çift heliks (Şekil 7b) yapısı elde edilir ki, bu, canlıların genetik yapı şifresi olan DNA moleküllerini modellemede kullanılır.
Sabun köpükleri ile ilgili iki temel kural vardır. Birincisi, eğer köpük kendisini destekleyen bir yüzey üzerinde ise bu yüzeye 900 açı yapacak şekilde birleşir. Düz bir yüzey üzerinde duran sabun köpüğü yarım küre şeklini alır ve her noktada destekleyen yüzey ile köpük yüzeyi 900 açılı olur. İkinci kural ise, eğer üç sabun köpüğü yüzeyi bir araya gelirse bir çizgi boyunda 1200 açı oluştururlar. Üç yüzeyin kesişmesi ile oluşan bu tip çizgilerden dört tanesi bir noktada bir araya gelirse, her iki çizgi arasındaki açı 1090 28’ 16’’ olur. Şekil 8’de bir tetrahedron çerçeve içerisinde oluşmuş bu tip yüzeyler gösterilmiştir.

900 ve 1200 açı prensiplerinin uygulanması ile matematikte önemli bir problem olan Steiner problemi çözülebilir. Steiner probleminde bir düzlemde verilen n adet noktayı birleştirecek en kısa yol ağı sorulmaktadır. Şeffaf iki düzlem, ince eşit uzunlukta paralel pimlerle birbirine bağlanarak bir sabun


eriyiğine daldırılır. Çıkarıldığında düzlem filmleri oluştuğu görülür. Bu filmler şeffaf destekleyen düzlemlerle 900 açılıdır ve her üç sabun filmi bir araya geldiğinde, birbirleri ile 1200 açı meydana getirirler. Yukarıdan bakıldığında, sabun filmi ile yüzeylerden birisinin kesişim çizgileri n sayıda noktayı birleştiren en kısa ağı verir. Şekil 9a’da 4 noktanın, Şekil 9b’de ise 5 noktanın nasıl birleştirildiği gösterilmiştir. Akıl ve şuurdan yoksun sabun köpüğünün karmaşık bir matematik problemi kendiliğinden çözebilmesi mümkün olmadığına göre, ona, bu mükemmel davranış özelliğinin kazandırıldığını kabul etmek gerekir.
Denizkestanesi ve denizyıldızı gibi bazı deniz canlılarının iskeletinde organik ve inorganik maddeleri ayıran duvarlarda periyodik tekrarlanan minimal alanlara rastlanmıştır. Şekil 10’da denizkestanesi iskeletinin mikro yapısı gösterilmiştir. Bu geometrinin çatlak ilerlemesini engelleyecek mükemmel yapıda şekillendirildiği tespit edilmiştir.
Sabun köpüğü deneyleri mimarlar için de ilham kaynağı olmuştur. Çatı ve çadır tasarımlarında bu tip deneylerden faydalanılmıştır. Bu konuda en önemli isimlerden birisi Alman mimar Frei Otto’dur. Frei Otto’nun bir düzleme monte ettiği iğne ve saç inceliğindeki iplikleri sabunlu suya batırarak elde ettiği minimal alanlar Şekil 11’de gösterilmiştir.
Bu tip bir sabun köpüğü modelinin mimarî yapıya dönüştürülebilmesi için dikkatlice fotoğrafı çekilir ve hassas ölçümler yapılır. Bundan sonra katı modeller yapılır ve rüzgâr tünellerinde denenir. Özel ölçüm âletleri ile rüzgâr ve kar yükü altında oluşabilecek gerilmeler tespit edilir. Gerçek yapıda saç teli iplikçiklerinin yerini yüksek mukavemete sahip ince çelik kablolar alır. Sabun köpüğü zarının yerini ise şeffaf plâstik sentetik malzemeler alır.
Şekil 12’de Münih’teki Olimpiyat Stadı’nın çatısı, Şekil 13’te Münih’teki Olimpiyat Atletik Arena’nın çatısı, Şekil 14’te ise yine aynı şehirdeki Olimpik Yüzme Arenası’nın çatısı gösterilmiştir. Bütün bu çatılar sabun köpüğü deneylerinden elde edilen minimal yüzeyler kullanılarak yapılmıştır.

Çocuklar, sabun köpüğü ile oynamayı çok severler; genelde yuvarlak bir çerçeveyi sabunlu suyun içerisine daldırıp çıkartarak üfler ve baloncukların uçuşunu seyrederler. Sabun köpüğü ve sabun filmleri ile oynayanlar sadece çocuklar değildir. Bilim adamları yüzyıllardır sabun köpükleri ile deneyler yapmakta, matematik teorileri geliştirmekte, değişik yüzeyler elde ederek bu konudaki bilgileri teknolojiye aktarmaktadırlar.

2) Bu çatılar kolayca yükseltilebilir, sökülebilir ve başka yere taşınabilirler. Klâsik binalar ise bir yerden başka bir yere kolayca taşınamaz;
3) Hemen her yerinde çekme gerilme kuvvetleri hâkim olan bu yapılar çok sağlamdır. Klâsik binalarda ise basma gerilmeleri çok yoğun olup bu tip gerilmeleri karşılamak üzere beton, tuğla gibi yapıyı aşırı ağırlaştıran malzemeler kullanılır.

Hafif ve sağlam malzeme yapıları canlılarda mükemmel bir tarzda kullanılmıştır. Buna, iskelet sistemimizin hafiflikle dayanıklılığı bir araya getirmesi, buğday, arpa gibi narin bitkilerin saplarındaki mükemmel dayanıklılık, sinek kanadının son derece ince ve elâstik yapısı gibi binlerce misâl verilebilir. Bu konuda daha detaylı bilgi, kaynak 2’de mevcuttur. Alman mimar Frei Otto’nun bu konudaki bir sözü mânidârdır: “Biyoloji mimarlık için vazgeçilmez hâle gelmiştir. Mimarlık da biyoloji için vazgeçilmez hâle gelmiştir.” Sabun köpüğü gibi cansız yapılarda da benzer mükemmelliklerin görülmesi tabiattaki kanunların aynı elden çıktığını göstermektedir.
Bilgisayar kapasitelerinin çok artması ile minimal yüzeyleri bulmak daha kolay hâle gelmiştir. Sabun köpüğü deneylerine alternatif olarak bilgisayarlarca hesaplanan ve çizilebilen son derece karmaşık minimal yüzeyler elde edilmiştir. Eğer insanlık olarak bilim ve teknolojide ilerlemek istiyorsak, etrafımızdaki basit ve önemsiz gibi görünen hâdiselere daha dikkatle ve tefekkürle bakmamız, Yaradan’ın bize sunduğu güzellikleri ve mükemmellikleri keşfetmemiz ve insanlığın hizmetine sunmamız gerekmektedir. Tasarımlarımız ne kadar tabiatta işletilen kurallara uyumlu ise, başarı şansımız o kadar artacaktır.
Kaynaklar
1. S. Hilderbrandt, A. Tromba, The Parsimonious Universe, Springer-Verlag, New York, 1996.
2. M. S. Polatöz, Tabiatta Mühendislik, Kaynak Yayınları, İzmir, 2003.
3. A. B. Smith, The stereom microstructure of the echinoid test. Special Papers in Palaeontology, 25, 1-85, 1981.
[SES]http://www.sizinti.com.tr/dosyalar/sesler/64kbps/350/4078.mp3[/SES]


 2Beğeni
2Beğeni